Prominencia

A prominencia dunha montaña, tamén denominada prominencia topográfica, altura de culminación, altura relativa, altura autónoma ou factor primario, é unha noción usada en orografía para a clasificación das montañas. Defínese como o desnivel mínimo que hai que descender desde o cume dunha montaña para ascender a outra, calquera que sexa, máis alta. Canto máis prominente sexa unha montaña máis destacará entre as que a rodean, con independencia da súa altitude.

As frechas verticais mostran a prominencia de tres picos nunha illa. Unha liña horizontal punteada liga cada pico, excepto o máis alto, ao momento máis baixo que hai que pasar para subir a outro máis alto que el; as curvadas, a relación de parentesco.

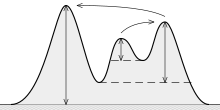
Todas as montañas, excepto o Everest, teñen unha montaña de maior altitude que elas (cume veciño máis alto o parent peak en inglés). E iso supón que debe existir algún lugar tal que para pasar dunha montaña a outra que sexa máis alta, pérdase a menor altitude posible. Esta sinxela observación, que xa foi estudada polo físico escocés James Clerk Maxwell, levoulle a pensar na existencia dunha relación inequívoca entre cada unha das cimas da superficie terrestre e unha portela. O aspecto máis complexo desta análise consiste en determinar cal é esa portela que relaciona ambas montañas.

Unha maneira de visualizar o concepto de prominencia consiste en imaxinar que se alaga a terra até a cima dun pico en cuestión. Por encima da auga asomarán, como illas, os cumes que sexan máis elevadas que ela. Agora comézase a baleirar a auga de modo que o seu nivel vai descendendo progresivamente. Nun momento dado observarase que se abriu unha lingua de terra seca que unirá o pico con outro que será máis alto que el. O valor de esa prominencia vén dada pola diferenza entre a altitude da montaña elixida e o nivel da auga nese instante.

A prominencia, do mesmo xeito que a altitude, é un valor absoluto para unha montaña, xa que unicamente depende do punto máis baixo que une unha montaña con calquera outra máis alta que ela.

O Denali, en Alaska, é un dos de maior prominencia do mundo (altitude: 6194 m, prominencia: 6138 m.

Historia

Aínda que visto desde Mittenwald (Alemaña), o Viererspitze (á izq.) é aparentemente alto, ten de feito unha altura de culminación ou prominencia moi pequena, duns 10 m.

A noción de prominencia apareceu para distinguir os cumes principais dos picos dos cumes secundarios nas listas exhaustivas que comezaron a ser establecidas polos coleccionistas de picos (os «peakbaggers»).

A finais do século XIX e principios do XX apareceron as primeiras listas de cumes por encima de certa altitude. En 1891, Hugh Munro publicou a lista de 538 picos escoceses de máis de 3.000 pés (914,4 m), das cales 283 poderían considerarse montañas separadas (as may fairly be considered as separate mountains) que se chamarán por el, munros. En 1911, o austríaco Karl Blodig reclamou ascender a todos os picos dos Alpes de máis de 4.000 m. Nestes dous casos non había un criterio explícito para distinguir os «verdadeiros cumes» daquelas que non estaban o suficientemente individualizadas como para estar na lista.

O primeiro en introducir a noción de prominencia (pero non a palabra) para delimitar unha lista foi John Rooke Corbett, quen estableceu na década de 1920 a lista de outeiros en Escocia de entre 2.500−3.000 pés (entre 762 e 914,4 m), retendo só aquelas con «unha caída de polo menos 500 pés en todos os lados» ("a drop at least 500 feet on all sides"). Esta lista de corbetts non foi publicada até 1952, despois da súa morte.

Despois do ascenso do pico Jongsong en 1930, Günter Oskar Dyhrenfurth comezou a enumerar picos de máis de 7.000 m, distinguindo entre montañas independentes, picos maiores e picos menores baseados ​​na« profundidade da portela». Estas listas foron publicadas no xornal Berge der Welt en colaboración co sueco Anders Bolinder.

A noción de «sela [de montar] relativa» foi introducida por Klaus Hormann en 1965. O concepto foi enseguida refinado e ampliado.

A cuestión tamén xurdiu nos Estados Unidos, para enumerar os «catorcemiles» (fourteener), é dicir, os picos de máis de 14.000 pés (4.267,4 m) de Colorado. En febreiro de 1968, William Graves propuxo en Trail and Timberline, o boletín do Colorado Mountain Club, como criterio para que un cume fose distinto, o que estivese separada dun cume máis alto por un paso inferior de polo menos 300 pés (saddledrop). Esa regra, que fixo posible atopar case a lista clásica, foi despois globalemente aceptada, aínda a pesar de que a lista máis común dos 54 «catorcemiles» inclúe o pico North Marroon e pico O Dente, que non cumpren con ese criterio.

O termo inglés prominence (prominencia) foi acuñado en 1981 polo estadounidense Stephen Fry, e utilizouno por primeira vez en 1987 nun artigo no que se definían as montañas ultramaiores (máis de 5.000 pés de prominencia), as montañas principais (máis de 1.000 pés), as montañas principais (entre 600−1.000 pés) e as montañas menores (entre 250−600 pés), con criterios adicionais sobre o abrupto das caras.

En 1992, Alan Dawson estableceu unha lista de todos os picos de Gran Bretaña de máis de 150 m de prominencia (independentemente da súa altitude), que chamaron marilyns.

En 1994, a Unión Internacional de Asociacións de Alpinismo (ou UIAA, por Union Internationale deas Associations d'Alpinisme) estableceu unha lista «oficial» de 82 picos alpinos de máis de 4.000 m, tendo en conta como «criterio topográfico» unha prominencia de 30 m, definida promediando os picos tangentes, e tamén porque representaba a lonxitude da corda no alpinismo clásico (o illamento topográfico tamén se podía ter en conta). Con todo, tamén se consideraron outros criterios, morfológicos e alpinísticos, e certos cumes que cumprían o criterio topográfico, como o Grand Xendarme do Weisshorn ou a Nez do Liskamm non se incluíron na lista, a diferenza do mont Blanc de Courmayeur e o Grand Pilier d'Angle que teñen só 10 m de prominencia.

Punto mínimo

Coñécese como punto mínimo (key col en inglés) ao momento máis baixo polo que hai que pasar para ir dun cume a calquera outro máis alto que el.

Este lugar adoita ser normalmente unha portela, pero pode ser unha paraxe de natureza ben distinta, como unha chaira, un barranco ou a superficie do mar.

Cume principal, Cume veciño máis alto e familias

O cume principal é o de maior elevación no sistema, pero, si hai outros de alturas similares, a forma de establecer cales son subcumes de cada un deles, xa que uns poden ser subcumes dos outros (na figura o pico do medio é un subcume do pico da dereita, o cal á súa vez é subcume do pico da esquerda que é o principal deste sistema, están marcados os puntos mínimos de cada un deles).

En relación ao cume veciño máis alto, defínense os conceptos de "familias" que relacionan un pico dado calquera co seu cume principal. Hai tres tipos de "familias": a prominence parentage, a height parentage e a encirclement parentage.

Cálculo da prominencia

A avaliación da prominencia consiste na determinación do punto mínimo que, como se dixo, relaciónase de maneira inequívoca cunha montaña (non pode haber dúas ou máis puntos mínimos posibles). Avaliada a altitude do punto mínimo, a prominencia vén dada por:

Prominencia = altitude montaña - altitude punto mínimo

As frechas verticais mostran a prominencia de tres picos nunha illa. Unha liña horizontal punteada liga cada pico, excepto o máis alto, ao momento máis baixo que hai que pasar para subir a outro máis alto que el.

A determinación da prominencia dunha montaña pode ser moi dificultosa xa que para cada montaña do planeta (a excepción do Everest) sempre hai outra máis alta que ela, pero en ocasións está a moitos quilómetros de distancia. Cando o punto mínimo está próximo á montaña en estudo, as cousas facilítanse moito.

A partir de modelos dixitais de elevacións (MDE) sería posible o desenvolvemento de algoritmos matemáticos para a avaliación da prominencia. Neste sentido, Edward Earl desenvolveu unha aplicación informática denominada WinProm que forneceu resultados satisfactorios en Estados Unidos e o Reino Unido. Doutra banda sistemas de información xeográfica, como GRASS, permiten realizar estes pesados cálculos.

Importancia do concepto de prominencia

O Amboto, de só 1.331.2 m e unha prominencia de 734 m, es máis importante que os picos del Infierno, de máis de 3.000 m

A prominencia é un dato tan importante ou máis que a altitude para determinar a importancia dunha montaña. É unha medida obxectiva que se correlaciona fortemente coa significación subxectiva dun cume. Dános idea da súa relevancia con referencia ás montañas que a rodean. Os picos de prominencia baixa adoitan ser picos subsidiarios doutros principais, en cambio unha prominencia alta asegura a relevancia da montaña e tenden a ser os puntos máis altos ao redor, adoitando ter excelentes vistas. Por exemplo, os Picos do Inferno, nos Pireneos, son tres cumes de máis de 3.000 m de altitude cada unha delas, pero moi próximas entre si, de tal forma que poden coroarse nunha mesma ascensión. O monte Amboto, de pouco máis de 1.300 m, sitúase solitario (o monte máis alto máis próximo é o Gorbea), polo que ten maior prominencia que calquera dos cumes dos Picos do Inferno. É dicir, o Amboto é máis importante na súa contorna que o pico do Inferno Central no seu.

Debido ao concepto de prominencia, as tres cimas secundarias do Kangchenjunga que están por encima dos 8.000 metros non adoitan figurar na listaxe oficial de ochomiles principais, xa que entre elas hai moi pouco desnivel (teñen pouca prominencia) ou o K2 (altura, 8.611 m; prominencia, 4.017 m) é considerada o segundo cume máis importante, por diante da antecima sur do Everest (altura, 8.749 m; prominencia, 10 m).

Situacións interesantes de prominencia

Os cumes principais e os puntos mínimos adoitan estar moitas veces cerca do pico a estudo, pero nas montañas importantes isto non adoita ser así e os estudos son complicados. Soamente cos modernos programas informáticos e a xestión de bases de datos xeográficas puidéronse resolver algunhas particularidades como as seguintes:

• O punto mínimo do Denali en Alaska (6194 m) é unha portela de 56 m que está cerca do lago Nicaragua.
• O monte Whitney (4421 m) ten o seu punto mínimo en Novo México nunha portela de 1.347 m de altitude que está a 1022 km de distancia do mesmo.
• O punto mínimo do monte Mitchell, teito dos Apalaches, está en Chicago.

Cuantificadores orométricos

O concepto de cuantificadores orométricos (Javier Urrutia, 2005), permite sistematizar o estudo de todas aquelas magnitudes que poden ser útiles á hora de avaliar a relevancia das montañas.

A partir da altitude e da prominencia desenvólvense outros cuantificadores orométricos que serven para expresar as propiedades métricas dunha montaña como a dominancia que é a relación entre a altitude e a prominencia, a potencia que relaciona a altitude, a prominencia e o punto mínimo, e outros moitos máis que axúdannos a definir obxectivamente unha determinada montaña.

Dominancia

Defínese a dominancia como a relación existente entre a prominencia e a altitude dunha montaña. Esta magnitude sinálanos que fracción da altitude do pico invístese, realmente, en darlle prominencia.

dominancia=prominencia·100/altitude

Con todo, este cuantificador non pode expresar a relevancia da elevación: un illote costeiro que se levante en Tenerife a 25 metros por encima do mar, ten unha altitude=prominencia=25 m e unha dominancia do 100%. Esta mesma dominancia é a que correspondería ao mesmo Teide.

Lista de montañas por prominencia

As vinte e cinco montañas de maior prominencia no mundo son as seguintes:

N.º	Pico	Localización	Altitude (m)	Prominencia (m)	Punto mínimo (m)	Cume veciño máis alto (prominencia)
1	Monte Everest	Nepal / China	8848	8848	0	ningún — máis alto do mundo
2	Aconcagua	Arxentina	6960,8	6960,8	0	ningún — máis alto de América
3	Denali (monte McKinley)	Estados Unidos (Alaska)	6194	6138	56	Aconcagua/ Nevado Ojos del Salado
4	Kilimanjaro	Tanzania	5895	5895	0	ningún — máis alto de África
5	Pico Cristóbal Colón / Pico Simón Bolívar	Colombia	5775	5584	191	Aconcagua
6	Monte Logan	Canadá (Yukón)	5959	5250	709	Denali (McKinley)
7	Pico de Orizaba	México	5636	4922	714	Monte Logan
8	Macizo Vinson	Antártida	4892	4892	0	ningún — máis alto de Antártida
9	Puncak Jaya	Indonesia (Nueva Guinea)	4884	4884	0	ningún — máis alto de Nova Guinea
10	Monte Elbrus	Rusia	5642	4741	901	Everest
11	Mont Blanc - Monte Bianco	Francia /  Italia	4808	4695	113	Everest
12	Monte Damavand	Irán	5610	4667	943	Elbrus
13	Kliuchevskoi	Rusia (Kamchatka)	4750	4649	101	Everest
14	Nanga Parbat	Paquistán	8125	4608	3517	Everest
15	Mauna Kea	Estados Unidos (Hawái)	4205	4205	0	ningún — máis alto da illa de Hawai
16	Jengish Chokusu	Kirguizistán / China	7439	4148	3291	Everest
17	Chimborazo	Ecuador	6268	4123	2145	Aconcagua
18	Bogda Feng	China	5445	4122	1323	Everest
19	Namcha Barwa	China (Tíbet)	7782	4106	3676	Everest
20	Monte Kinabalu	Malaisia	4095	4095	0	ningún — máis alto de Borneo
21	Monte Rainier	Estados Unidos (Washington)	4393	4023	370	Orizaba / Denali (McKinley)
22	K2	Paquistán / China	8611	4017	4594	Everest
23	Monte Nivel Deixen	Etiopía	4550	3997	553	Kilimanjaro
24	Volcán Tajumulco	Guatemala	4220	3980	240	Orizaba / Denali (McKinley)
25	Pico Bolívar	Venezuela	4981	3957	1024	Chimborazo / Aconcagua

Véxase tamén

• Altitude
• Relevancia (orografía)
• Pico ultraprominente
• Eminencia
• Portela

= Ligazóns externas

En castelán

• Conceptos sobre prominencia.

En inglés

• K2 prominence
• http://www.peaklist.org a website about mountain prominence, with lists and/or maps covering the entire world down to 1500m of prominence (the "ultras")
• Prominence and Orometry a detailed and lucide account by Aaron Maizlish of the theory of prominence
• http://groups.yahoo.com/group/prominence/ Yahoo! Groups, Topographic prominence discussion
• Edward Earl’s website
• Edward Earl’s article on Topographic Prominence
• Index to definitions in the Canadian Mountain Encyclopedia
• Mountain Hierarchies a description of the different systems of defining parent peak
• Mountain Hierarchy using Prominence Islands
• Surface Network Modelling on the Center for Advanced Surface Analysis website
• Surface Network Modelling a paper by Sanjay Ra and Jeremy Morley
• The 100 most prominent peaks in Colorado
• Alan Dawson's The Relative Hills of Britain