Automorfismo

En matemáticas, un automorfismo é un isomorfismo dun obxecto matemático en si mesmo. É, en certo sentido, unha simetría do obxecto e unha forma de mapear o obxecto en si mesmo conservando toda a súa estrutura. O conxunto de todos os automorfismos dun obxecto forma un grupo, chamado grupo de automorfismos.

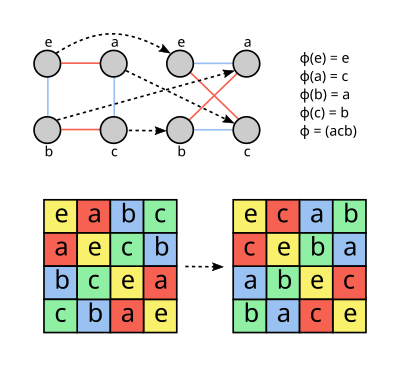
Definición editar

Nunha estrutura alxébrica como un grupo, un anel ou espazo vectorial, un automorfismo é simplemente un homomorfismo bixectivo dun obxecto en si mesmo.

Para un obxecto dalgunha categoría, un automorfismo é un morfismo do obxecto en si mesmo que ten un morfismo inverso; é dicir, un morfismo $f:X\to X$ é un automorfismo se hai un morfismo $g:X\to X$ tal que $g\circ f=f\circ g=\operatorname {id} _{X},$ onde $\operatorname {id} _{X}$ é o morfismo de identidade de $X$ .

Grupo de automorfismos editar

Os automorfismos dun obxecto $X$ forman un grupo baixo composición de morfismos, que se chama grupo de automorfismos de $X$ .

O grupo de automorfismos dun obxecto $X$ nunha categoría $C$ denomínase a miúdo $Aut C (X)$ , ou simplemente Aut (X) se a categoría esta clara no contexto.

Exemplos editar

En teoría de conxuntos, unha permutación arbitraria dos elementos dun conxunto X é un automorfismo. O grupo de automorfismos de X tamén se chama o grupo simétrico en X.
En aritmética elemental, o conxunto de enteiros, Z, considerado como un grupo baixo adición, ten un automorfismo non trivial único: a negación. Porén, considerado como un anel, só ten o automorfismo trivial. En xeral, a negación é un automorfismo de calquera grupo abeliano, pero non dun anel ou dun corpo.
Un automorfismo de grupo é un isomorfismo de grupos dun grupo en si mesmo. Informalmente, é unha permutación dos elementos do grupo de tal xeito que a estrutura permanece inalterada. Para cada grupo G hai un homomorfismo de grupo natural G → Aut(G) cuxa imaxe é o grupo Inn(G) de automorfismos internos e cuxo kernel é o centro de G Así, se G ten un centro trivial pode ser inserido no seu propio grupo de automorfismos.^[1]
En álxebra linear, un endomorfismo dun espazo vectorial V é un operador lineal V → V. Un automorfismo é un operador linear invertible en V. Cando o espazo vectorial é de dimensión finita, o grupo de automorfismos de V é o mesmo que o grupo linear xeral GL(V).
Un automorfismo de corpos é un homomorfismo de anel bixectivo dun corpo en si mesmo.
- O corpo $\mathbb {Q}$ dos números racionais non ten outro automorfismo que a identidade, xa que un automorfismo debe fixar a identidade aditiva $0$ e a identidade multiplicativa $1$ .
- O corpo $\mathbb {R}$ dos números reais non ten outro automorfismo que a identidade.
- O corpo $\mathbb {C}$ dos números complexos, ten un único automorfismo non trivial, que envía $\mathbb {R}$ a $\mathbb {R} ,$ a conxugación complexa. Por outro lado, hai infinitamente moitos (incontables) automorfismos, se asumimos o axioma de escolla.^[2]^[3]
- O estudo dos automorfismos das extensións de campo alxébrico é o punto de partida e o principal obxecto da Teoría de Galois.
O grupo de automorfismos dos cuaternións (H) como un anel son os automorfismos internos, polo teorema de Skolem-Noether son os mapas da forma a ↦ bab⁻¹.^[4] Este grupo é isomorfo a SO (3), o grupo de rotacións no espazo tridimensional.
O grupo de automorfismos dos octonións (O) é o grupo de Lie G<sub id="mwng">2</sub>.
En teoría de grafos un automorfismo dun grafo é unha permutación dos nodos que conserva arestas e non arestas. En particular, se dous nodos están unidos por unha aresta, tamén o están as súas imaxes baixo a permutación.
En xeometría, un automorfismo pode ser chamado un movemento no espazo. Tamén se usa terminoloxía especializada:
- En espazo métrico un automorfismo é unha auto-isometría. O grupo de automorfismos tamén se chama o grupo de isometrías.
- Na categoría dsa superficies de Riemann, un automorfismo é un mapa biholomorfo (tamén chamado a mapa conforme), dunha superficie en si mesma. Por exemplo, os automorfismos da esfera de Riemann son transformacións de Möbius.
- Un automorfismo dunha variedade M é un difeomorfismo de M en si mesmo. O grupo de automorfismos denótase Diff(M).
- En topoloxía, os morfísmos entre espazos topolóxicos son chamados mapas continuos, e un automorfismo dun espazo topolóxico é un homeomorfismo do espazo en si mesmo, ou auto-homeomorfismo (ver grupo de homeomorfismos). Neste exemplo non é abondo que un morfismo sexa bixectivo para ser un isomorfismo.

Automorfismos internos e externos editar

Nalgunhas categorías, en particular grupos, aneis e álxebras de Lie, é posible separar os automorfismos en dous tipos, chamados automorfismos "interiores" e "exteriores". Nalgunhas categorías, en particular grupos, aneis e álxebras de Lie, é posible separar os automorfismos en dous tipos, chamados automorfismos "interiores" e "exteriores".

No caso dos grupos, os automorfismos internos son as conxugacións polos elementos do propio grupo. Para cada elemento a dun grupo G, a conxugación por a é a operación φ_a : G → G dada por φ_a(g) = aga⁻¹ (ou a⁻¹ ga). Pódese comprobar facilmente que a conxugación por a é un automorfismo de grupo. Os automorfismos internos forman un subgrupo normal de Aut( G ), denotado por Inn(G); isto chámase lema de Goursat.

Os outros automorfismos chámanse automorfismos externos. O grupo cociente Aut(G) / Inn(G) adoita denotarse por Out(G); os elementos non triviais son as coclases (cosets) que conteñen os automorfismos exteriores.

A mesma definición vale para calquera anel ou álxebra onde $a$ é calquera elemento invertible. Para as álxebras de Lie a definición é lixeiramente diferente.

Notas editar

↑ PJ Pahl, R Damrath (2001). "§7.5.5 Automorphisms". Mathematical foundations of computational engineering (Felix Pahl translation ed.). Springer. p. 376. ISBN 3-540-67995-2.
↑ Yale, Paul B. (May 1966). Automorphisms of the Complex Numbers (PDF). Mathematics Magazine 39. pp. 135–141. JSTOR 2689301. doi:10.2307/2689301.
↑ Lounesto, Pertti (2001). Clifford Algebras and Spinors (2nd ed.). Cambridge University Press. pp. 22–23. ISBN 0-521-00551-5.
↑ Handbook of algebra 3. Elsevier. 2003. p. 453.

Véxase tamén editar

Outros artigos editar

Ligazóns externas editar

[Pahl-1] PJ Pahl, R Damrath (2001). "§7.5.5 Automorphisms". Mathematical foundations of computational engineering (Felix Pahl translation ed.). Springer. p. 376. ISBN 3-540-67995-2.

[2] Yale, Paul B. (May 1966). Automorphisms of the Complex Numbers (PDF). Mathematics Magazine 39. pp. 135–141. JSTOR 2689301. doi:10.2307/2689301.

[3] Lounesto, Pertti (2001). Clifford Algebras and Spinors (2nd ed.). Cambridge University Press. pp. 22–23. ISBN 0-521-00551-5.

[4] Handbook of algebra 3. Elsevier. 2003. p. 453.

[1]

[2]

[3]

[4]