Media (estatística)
En matemáticas e estatística unha media é unha medida de tendencia central. Existen distintos tipos de medias, tales como a media xeométrica, a media ponderada e a media harmónica aínda que na linguaxe común, o termo refírese xeralmente á media aritmética.

Exemplos de medias
editarExisten numerosos exemplos de medias . Unha das poucas propiedades compartidas por todas as medias é que calquera media está comprendida entre o valor máximo e o valor mínimo do conxunto de variables:
Ademais debe cumprirse que:
Media aritmética
editarA media aritmética é unha media estándar que a miúdo se denomina simplemente "media".[1]
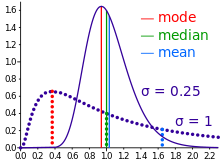
A media confúndese ás veces coa mediana ou a moda. A media aritmética é a media dun conxunto de valores, ou a súa distribución; con todo, para as distribucións con nesgo, a media non é necesariamente o mesmo valor que a mediana ou que a moda. A media, moda e mediana son parámetros característicos dunha distribución de probabilidade. É ás veces unha forma de medir o nesgo dunha distribución tal e como se pode facer nas distribucións exponencial e de Poisson.
Por exemplo, a media aritmética de 34, 27, 45, 55, 22 e 34 (seis valores) é
Media aritmética ponderada
editarÁs veces pode ser útil outorgar pesos ou valores aos datos dependendo da súa relevancia para determinado estudo. Neses casos pódese utilizar unha media ponderada. Se é un conxunto de datos ou media muestral e son números reais positivos, chamados "pesos" ou factores de ponderación, defínese a media ponderada relativa a eses pesos como:
A media é invariante fronte a transformacións lineares, cambio de orixe e escala, das variables, é dicir se X é unha variable aleatoria e Y é outra variable aleatoria que depende linearmente de X, é dicir, Y = a·X + b (onde a representa a magnitude do cambio de escala e b a do cambio de orixe) tense que:
Media xeométrica
editarA media xeométrica é unha media moi útil en conxuntos de números que son interpretados en orde do seu produto, non da súa suma (tal e como ocorre coa media aritmética). Por exemplo, as velocidades de crecemento.
Por exemplo, a media xeométrica da serie de números 34, 27, 45, 55, 22 e 34 (seis valores) é
Media harmónica
editarA media harmónica é unha media moi útil en conxuntos de números que se definen en relación con algunha unidade, por exemplo a velocidade (distancia por unidade de tempo).
Por exemplo, a media harmónica dos números: 34, 27, 45, 55, 22, e 34 é
Xeneralizacións da media
editarExisten diversas xeneralizacións das medias anteriores.
Media xeneralizada
editarAs medias xeneralizadas, tamén coñecidas como medias de Hölder, son unha abstracción das medias cuadráticas, aritméticas, xeométricas e harmónicas. Defínense e agrúpanse a través da seguinte expresión:
Escollendo un valor apropiado do parámetro m, tense:
- - máximo,
- - media cuadrática,
- - media aritmética,
- - media xeométrica,
- - media harmónica,
- - mínimo.
Media-f xeneralizada
editarEsta media pode xeneralizarse para unha función monótona como a media-f xeneralizada:
onde é unha función inxectiva e un intervalo. Escollendo formas particulares para obtéñense algunhas das medias máis coñecidas:
- - media aritmética,
- - media harmónica,
- - media xeneralizada,
- - media xeométrica, .
Media dunha función
editarPara unha función continua sobre un intervalo [a,b], pódese calcular o valor medio da función sobre [a,b] como:
De feito a definición anterior cúmprese tamén para unha función limitada aínda que non sexa continua, coa condición de que sexa medible.
Media estatística
editarA media estatística emprégase en estatística para dous conceptos diferentes aínda que numericamente similares:
- A media da mostra, que é un estatístico que se calcula a partir da media aritmética dun conxunto de valores dunha variable aleatoria.
- A media da poboación, valor esperado ou esperanza matemática dunha variable aleatoria.
Na práctica dada unha mostra estatística suficientemente grande o valor da media muestral da mesma é numericamente moi próximo á esperanza matemática da variable aleatoria medida nesa mostra. O devandito valor esperado, só é calculable se se coñece con toda exactitude a distribución de probabilidade, cousa que raramente sucede na realidade, e por esa razón, a efectos prácticos a chamada media refírese normalmente á media da mostra.
Media da mostra
editarA media da mostra é unha variable aleatoria, xa que depende da mostra, aínda que é unha variable aleatoria en xeral cunha varianza menor que as variables orixinarias empregadas no seu cálculo. Se a mostra é grande e está ben escollida, pode tratarse a media da mostra como un valor numérico que aproxima con precisión a media de poboación, que caracteriza unha propiedade obxectiva da poboación. Defínese como segue: se se ten unha mostra estatística de valores de valores para unha variable aleatoria X con distribución de probabilidade F(x, θ) [onde θ é un conxunto de parámetros da distribución] defínese a media da mostra n-ésima como:
Media da poboación
editarA media da poboación tecnicamente non é unha media senón un parámetro fixo que coincide coa esperanza matemática dunha variable aleatoria. O nome "media da poboación" emprégase para indicar que valor numérico dunha media muestral é numericamente próximo ao parámetro media da poboación, para unha mostra adecuada e suficientemente grande.
Notas
editar- ↑ Definicións no Dicionario da Real Academia Galega e no Portal das Palabras para medio. 12ª acepción