Hipérbole (xeometría)

Este artigo trata sobre a curva. Para o recurso estilístico véxase: Hipérbole.

Unha hipérbole (do grego ὑπερβολή) é unha sección cónica, unha curva aberta de dúas pólas obtida de cortar un cono recto por un plano oblicuo ao eixe de simetría cun ángulo menor que o da xeratriz respecto do eixe de revolución.

As asíntotas da hipérbole son as liñas descontinuas azuis que se cortan no centro da hipérbole (curvas rubias), C. Os dous puntos focais denomínanse F₁ e F₂, e a liña negra que os une é o eixe transversal. A liña fina perpendicular en negro que pasa polo centro é o eixe conxugado, mentres que as dúas liñas grosas en negro paralelas ao eixe conxugado (ou perpendiculares ao eixe transversal) son as dúas directrices, D₁ e D₂. A excentricidade e (e>1), é igual ao cociente entre as distancias (en verde) desde un punto P da hipérbole até un dos focos e a súa correspondente directriz. Os dous vértices atópanse no eixe transversal a unha distancia ±a con respecto ao centro.

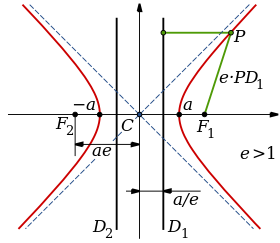
Unha hipérbole é o lugar xeométrico dos puntos dun plano tales que o valor absoluto da diferenza das súas distancias a dous puntos fixos, chamados focos, é igual á distancia entre os vértices, que é unha constante positiva.

Etimoloxía

Seccións cónicas.

Hipérbole deriva da verba grega ὑπερβολή (exceso), e é cognado de hipérbole (a figura literaria que equivale a esaxeración).

Historia

Debido á inclinación do corte, o plano da hipérbole interseca ambas ramas do cono.

Segundo a tradición, as seccións cónicas foron descritas por primeira vez por Menecmo, no seu estudo do problema da duplicación do cubo, onde demostra a existencia dunha solución mediante o corte dunha parábola cunha hipérbole, o cal é confirmado posteriormente por Proclo e Eratóstenes.

Mais o primeiro en usar o termo de hipérbole foi Apolonio de Perge no seu tratado Cónicas, considerada a obra maior sobre o tema das matemáticas gregas, e onde se desenvolve o estudo das tanxentes das seccións cónicas.

Ecuacións da hipérbole

Ecuacións en coordenadas cartesianas:

Ecuación dunha hipérbole con centro na orixe de coordenadas $(0,0)\,$ (forma canónica). $a\,$ é o semieixo maior (metade da distancia entre as dúas pólas), e $b\,$ é o semieixo menor.

${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1$

Ecuación dunha hipérbole con centro en $(h,k)\,$

${\frac {(x-h)^{2}}{a^{2}}}-{\frac {(y-k)^{2}}{b^{2}}}=1$

Ecuación da hipérbole na súa forma complexa:

Unha hipérbole no plano complexo é o lugar xeométrico formado por un conxunto de puntos $z\,$ (complexos), no plano $ReIm\,$; tales que, calquera deles satisfai a condición xeométrica de que o valor absoluto da diferenza das súas distancias $|z-w_{1}|-|z-w_{2}|\,$, a dous puntos fixos chamados focos$w_{1}\,$ e $w_{2}\,$, é unha constante positiva igual ao dobre da distancia (é dicir, $2l\,$ ) que existe entre o seu centro e calquera dos seus vértices do eixe focal.

A ecuación queda: $|z-w_{1}|-|z-w_{2}|=2l\,$

Ecuacións en coordenadas polares:

Dúas hipérboles e as súas asíntotas.

Hipérbole aberta de dereita a esquerda:

$r^{2}=a\sec 2\theta \,$

Hipérbole aberta de arriba a abaixo:

$r^{2}=-a\sec 2\theta \,$

Hipérbole aberta de nordeste a suroeste:

$r^{2}=a\csc 2\theta \,$

Hipérbole aberta de noroeste a sueste:

$r^{2}=-a\csc 2\theta \,$

Ecuacións paramétricas:

Hipérbole aberta de dereita a esquerda:

${\begin{matrix}x=a\sec t+h\\y=b\tan t+k\\\end{matrix}}\qquad \mathrm {o} \qquad {\begin{matrix}x=\pm a\cosh t+h\\y=b\sinh t+k\\\end{matrix}}$

Hipérbole aberta de arriba a abaixo:

${\begin{matrix}x=a\tan t+h\\y=b\sec t+k\\\end{matrix}}\qquad \mathrm {o} \qquad {\begin{matrix}x=a\sinh t+h\\y=\pm b\cosh t+k\\\end{matrix}}$

En todas as formulas (h,k) son as coordenadas do centro da hipérbole, a é a lonxitude do semieixe maior, b é a lonxitude do semieixe menor.

Véxase tamén

Ligazóns externas

• Animación dun plano seccionando un cono e determinando a curva cónica hipérbole (en castelán)
• Derivación da hipérbole de Apollonius en Convergence (en inglés)