Función de Thomae
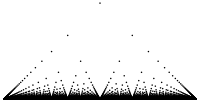
A Función de Thomae, chamada así en honra a Carl Johannes Thomae, tamén coñecida como a función das pipocas, a función gotas de choiva, a función das nubes numerables, a función modificada de Dirichlet, a función da regra[1], ou as estrelas sobre Babilonia (por John Horton Conway) é unha modificación da función de Dirichlet. O valor real da función f(x) defínese como segue:
onde:
- ℚ é o conxunto dos números racionais
- ℕ é o conxunto dos números naturais
- ℤ é o conxunto dos números enteiros
- mcd é o máximo común divisor
Se x = 0, tómase q = 1. Asumindo que o mcd(p, q) = 1 e q > 0 dá unha representación única do número racional (exemplo, excluíndo a representación de 2/4 como 1/2) facendo de f unha función ben definida.
Descontinuidades
editarA función das pipocas é talvez o exemplo máis simple dunha función cun complexo conxunto de descontinuidades: f é continua en todos os números irracionais e descontinua en todos os números racionais.
Demostración informal
editarClaramente, f é descontinua en todos os racionais: desde que os irracionais son densos nos reais, para algún racional 'x', sen importar que se elixa, podemos atopar un irracional 'a' a unha distancia menor que onde f(a) = 0 (pero f(x) é positivo). Noutras palabras, f non se pode aproximar a calquera número positivo, xa que o seu codominio está cheo de ceros.
Para mostrar a continuidade nos irracionais, sen perda de xeneralidade supomos que é racional (para algún irracional podemos optar por unha racional máis pequena e a proba é transitiva). Posto que é racional, pode ser expresada en termos máis sinxelos como a/b. Queremos mostrar que f é continua en 'x' cando 'x' é irracional.
Note que f toma o seu valor máximo de 1 en cada número enteiro, polo que podemos restrinxir o noso estudo entre e . Como ten un denominador finito b, os únicos valores para os que f pode devolver un valor maior a son os que teñen un denominador menor ou igual a b. Non só existe un número finito de valores entre dous enteiros con denominador menor ou igual que b, polo que estes pódense enumerar de maneira exhaustiva. Elixindo como a distancia máis pequena próxima de 'x' a un destes valores garante que todos os valores cunha distancia menor teñan f(x) < .
Integrabilidade
editarA función é Riemann integrable[2] baixo o seguinte criterio:
|
Ademais, o conxunto de descontinuidades son os números racionais, e os racionais son numerables, o conxunto ten medida cero, polo que a función no [0, 1], verifica o criterio de Lebesgue, e por tanto é Riemann integrable no [0, 1].
Seguimento
editarUnha pregunta natural é se hai unha función continua nos números racionais e descontinua nos números irracionais. Isto é imposible porque o conxunto de descontinuidades dunha función debe ser un conxunto , unión numerable de conxuntos pechados. Se tal función existise, os irracionais serían un conxunto e por tanto, xa que non conteñen un intervalo, serían un conxunto escaso. Como os números reais, son a unión de racionais e irracionais, serían un conxunto escaso. Isto contradi o Teorema de categoría de Baire.
Unha variante da función das pipocas pode ser usada para mostrar que calquera conxunto de números reais pode ser un conxunto de descontinuidades dunha función. Se é a unión numerable de conxuntos pechados , definimos
Un argumento similar ao utilizado para a función das pipocas mostra que ten a A como conxunto de descontinuidades.
Notas
editarVéxase tamén
editarBibliografía
editar- Robert G. Bartle and Donald R. Sherbert (1999), Introdución á Análise Real, 3.ª Edición (Exemplo 5.1.6 (h)). Wiley. ISBN 978-0-471-32148-4
- Spivak, M. Cálculo en variedades. 1965. Perseus Books. ISBN 0-8053-9021-9
- Abbot, Stephen. Entendendo Análise. Berlín: Springer, 2001. ISBN 0-387-95060-5
