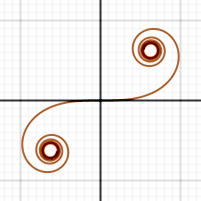
Clotoide

A espiral de Cornu, tamén coñecida como clotoide e como espiral de Euler e radioide de arcos, é unha curva cuxa curvatura varía linealmente ao longo da súa lonxitude. A espiral de Cornu foi creada por Marie Alfred Cornu como un nomograma para os cálculos de difracción en ciencia e enxeñería. Nos proxectos de enxeñería de estradas, esta espiral úsase amplamente como curva de transición co obxectivo principal de conectar xeométricamente unha liña recta e unha curva circular. Esta curva garante unha diminución lineal da curvatura co camiño seguido ao longo do seu desenvolvemento, proporcionando así unha variación gradual do raio de curvatura. Isto resulta entón:

• A súa curvatura comeza en cero no punto de osculación con aliñación recta e aumenta linealmente a medida que se desenvolve a curva.
• Cando a espiral/clotoide se atopa coa curva circular no seu punto de osculación, a súa curvatura é igual á da curva circular.

Espiral de Cornu

A espiral de Cornu xérase polo debuxo paramétrico de S (x) contra C (x), onde:

$S(x)=\int _{0}^{x}\sin(t^{2})\,dt=\sum _{n=0}^{\infty }(-1)^{n}{\frac {x^{4n+3}}{(4n+3)(2n+1)!}},$

$C(x)=\int _{0}^{x}\cos(t^{2})\,dt=\sum _{n=0}^{\infty }(-1)^{n}{\frac {x^{4n+1}}{(4n+1)(2n)!}}.$

{C (x), S (x)} (Nótese que a espiral converxe cara ao centro dos buratos da imaxe superior cando x tenta a infinito e a menos infinito.)

Seguindo a curva, a lonxitude da curva de {S (0), C (0)} a {S (x), C (x)} debe ser igual a x, xa que S ′ (x )² + C ′ (x)² = 1. A lonxitude total da curva (de x = −∞ a ∞) é, polo tanto, infinito.

Véxase tamén

Ligazóns externas

• http://hyperphysics.phy-astr.gsu.edu/hbase/phyopt/cornu.html#c1
• Loopings das montañas rusas: non son circulares senón clotoides, para evitar que a xente se desmaie polas forzas G de aceleración (microsiervos.com; en castelán e vídeo en inglés)