Distribución lognormal

Para outras páxinas con títulos homónimos véxase: Distribución.

Log-normal

Función de densidade μ=0
Función de distribución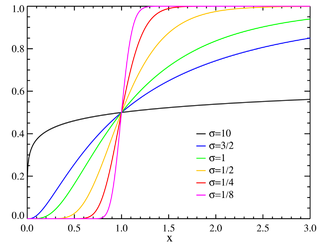 μ=0
Parámetros	$s\geq 0$ $-\infty \leq \mu \leq \infty$
Soporte	$x\in [0;+\infty )\!$
Función de densidade	${\frac {e^{-[{\frac {\ln(x)-\mu }{\sigma }}]^{2}/2]}}{x\sigma {\sqrt {2\pi }}}}$
Función de distribución	${\frac {1}{2}}+{\frac {1}{2}}\mathrm {Erf} \left[{\frac {\ln(x)-\mu }{\sigma {\sqrt {2}}}}\right]$
Media	$e^{\mu +\sigma ^{2}/2}$
Mediana	$e^{\mu }$
Moda	$e^{\mu -\sigma ^{2}}$
Varianza	$(e^{\sigma ^{2}}\!\!-1)e^{2\mu +\sigma ^{2}}$
Asimetría	$e^{-\mu -\sigma ^{2}/2}(e^{\sigma ^{2}}\!\!+2){\sqrt {e^{\sigma ^{2}}\!\!-1}}$
Curtose	$e^{4\sigma ^{2}}\!\!+2e^{3\sigma ^{2}}\!\!+3e^{2\sigma ^{2}}\!\!-6$
Entropía	${\frac {1}{2}}+{\frac {1}{2}}\ln(2\pi \sigma ^{2})$
F. xeradora de momentos	(ver no texto os momentos)
Func. caract.

En probabilidade e estatística, a distribución log-normal é a distribución de probabilidade de calquera variable aleatoria con seu logaritmo normalmente distribuído (a base da función logarítmica non é importante xa que se log_a X está distribuída normalmente se e só se log_b X está distribuída normalmente). Se X é unha variable aleatoria cunha distribución normal, entón exp(X) ten unha distribución log-normal.

"Log-normal" tamén se escribe "log normal" ou "lognormal".

Unha variable pode ser modelada como log-normal se pode ser considerada como o produto multiplicativo de moitos pequenos factores independentes. Un exemplo típico é o retorno a longo prazo dunha inversión nunha acción: pódese considerar como o produto dos retornos diarios.

A distribución log-normal ten a función densidade de probabilidade

$f(x;\mu ,\sigma )={\frac {1}{x\sigma {\sqrt {2\pi }}}}e^{-(\ln x-\mu )^{2}/2\sigma ^{2}}$

para $x>0$, onde $\mu$ e $\sigma$ son a media e o desvío estándar do logaritmo da variable. O valor esperado é

$\mathrm {E} (X)=e^{\mu +\sigma ^{2}/2}$

e a varianza é

$\mathrm {var} (X)=(e^{\sigma ^{2}}-1)e^{2\mu +\sigma ^{2}}$.

Relación coa media e o desvío estándar xeométrico

A distribución log-normal, a media xeométrica, e o desvío estándar xeométrico están relacionadas. Neste caso, a media xeométrica é igual a $\exp(\mu )$ e o desvío estándar xeométrico é igual a$\exp(\sigma )$.

Se unha mostra de datos determinase que provén dunha poboación distribuída seguindo unha log-normal, a media xeométrica e o desvío estándar xeométrico pódense utilizar para estimar os intervalos de confianza tal como a media aritmética e o desvío estándar se usan para estimar os intervalos de confianza para un dato distribuído normalmente.

Límite do intervalo de confianza	espazo log	xeométrica
3σ límite inferior	$\mu -3\sigma$	$\mu _{\mathrm {geo} }/\sigma _{\mathrm {geo} }^{3}$
2σ límite inferior	$\mu -2\sigma$	$\mu _{\mathrm {geo} }/\sigma _{\mathrm {geo} }^{2}$
1σ límite inferior	$\mu -\sigma$	$\mu _{\mathrm {geo} }/\sigma _{\mathrm {geo} }$
1σ límite superior	$\mu +\sigma$	$\mu _{\mathrm {geo} }\sigma _{\mathrm {geo} }$
2σ límite superior	$\mu +2\sigma$	$\mu _{\mathrm {geo} }\sigma _{\mathrm {geo} }^{2}$
3σ límite superior	$\mu +3\sigma$	$\mu _{\mathrm {geo} }\sigma _{\mathrm {geo} }^{3}$

Onde a media xeométrica $\mu _{\mathrm {geo} }=\exp(\mu )$ e o desvío estándar xeométrico $\sigma _{\mathrm {geo} }=\exp(\sigma )$

Momentos

Os primeiros momentos son:

$\mu _{1}=e^{\mu +\sigma ^{2}/2}$

$\mu _{2}=e^{2\mu +4\sigma ^{2}/2}$

$\mu _{3}=e^{3\mu +9\sigma ^{2}/2}$

$\mu _{4}=e^{4\mu +16\sigma ^{2}/2}$

ou de forma xeral:

$\mu _{k}=e^{k\mu +k^{2}\sigma ^{2}/2}.$

Estimación de parámetros Maximum likelihood

Para determina-los estimadores que máis aproximan os parámetros μ e σ da distribución log-normal, podemos utilizar o mesmo procedemento que para a distribución normal. Para non repetilo, obsérvese que

$f_{L}(x;\mu ,\sigma )={\frac {1}{x}}\,f_{N}(\ln x;\mu ,\sigma )$

onde por $f_{L}(\cdot )$ denotamos a función de densidade de probabilidade da distribución log-normal, e por $f_{N}(\cdot )$— a da distribución normal. Polo tanto, utilizando os memos índices para denotar as distribucións, podemos escribir que

${\begin{matrix}\ell _{L}(x_{1},x_{2},...,x_{n};\mu ,\sigma )&=&-\sum _{k}\ln x_{k}+\ell _{N}(\ln x_{1},\ln x_{2},...,\ln x_{n};\mu ,\sigma )=\\\ &=&\operatorname {const} (\mu ,\sigma )+\ell _{N}(\ln x_{1},\ln x_{2},...,\ln x_{n};\mu ,\sigma ).\end{matrix}}$

Xa que o primeiro termo é constante respecto a μ e σ, ambas funcións logarítmicas, $\ell _{L}$ e $\ell _{N}$, obteñen o seu máximo co mesmo μ e σ. Polo tanto, utilizando as fórmulas para os estimadores dos parámetros da distribución normal, e a inigualdade de arriba, deducimos que para a distribución log-normal cúmprese

${\widehat {\mu }}={\frac {\sum _{k}\ln x_{k}}{n}},\ {\widehat {\sigma }}^{2}={\frac {\sum _{k}{\left(\ln x_{k}-{\widehat {\mu }}\right)^{2}}}{n}}.$

Distribución relacionadas

• $Y\sim N(\mu ,\sigma ^{2})$ é unha distribución normal se $Y=\ln(X)$ e $X\sim \operatorname {Log-N} (\mu ,\sigma ^{2})$.
• Se $X_{m}\sim \operatorname {Log-N} (\mu ,\sigma _{m}^{2}),\ m={\overline {1...N}}$ son variables independentes log-normalmente distribuídas co mesmo parámetro μ e permitindo que varie σ, e $Y=\prod _{m=1}^{N}X_{m}$, entón Y é unha variable distribuída log-normalmente como: $Y\sim \operatorname {Log-N} \left(\mu ,\sum _{m}\sigma _{m}^{2}\right)$.

Véxase tamén

Outros artigos

• Media xeométrica
• Desvío estándar xeométrico
• Función error